Seeing ripples on walls
A stone dropped in a quiet pond creates ripples that propagate outward from the stone's "impact" location. The resulting waves on the water's surface are a visual cue that lets the viewer infer where the stone was dropped. Moreover, the shape and amplitude of the resulting waves convey additional cues about the water-stone interaction, such as the height from which the stone was dropped (from the wave's amplitude).

But similar interactions, where an object's impact creates transient surface waves, happen all around us. Examples include a ping-pong ball striking a table during a game, a person's footsteps, or someone knocking on the other side of the door or wall. But unlike the quiet pond example above, the waves created from all these ubiquitous physical interactions are too subtle to be perceived with our eyes and most cameras.
But what can we tell about the environment if we could see these resulting surface waves?


Localizing impacts beyond the line of sight
An object hitting a surface creates transient elastic waves propagating from the impact location.
These waves manifest as transient surface vibrations. By imaging these vibrations, at only a sparse set of surface points, we can computationally invert a wave propagation model and recover the impact source location. This means we can localize impacts beyond the line of sight (of the impact source) as long as the resulting surface vibrations as observable.
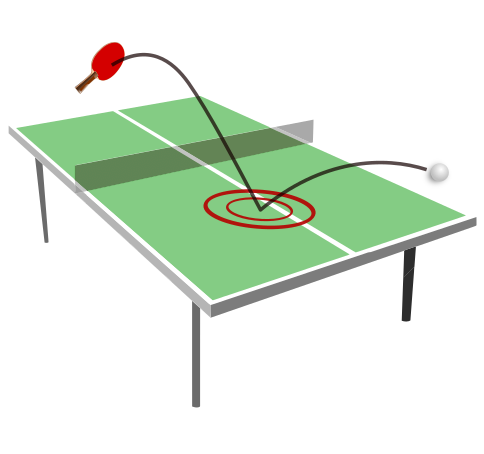
For example, in the experiment below, we set our camera to image the surface vibrations at five points from below the ping pong table's surface. Then, by observing the surface vibrations, our system can localize where the ball strikes the table, during play.
Ping pong table experiment. Our camera images the surface vibrations at five points at the bottom of the ping pong table. The point's bottom surface locations are visualized by the five markers seen on the top surface. From the observed vibrations, we localize the ball's impact location during a game. We visualize the recovered ball strike locations using two concentric red circles.
And in this experiment, we image the floor vibrations and localize the footsteps of the walking person.
Footsteps experiment. Our camera is located on the left staircase and images five points on the floor. From the observed vibrations, we localize the person's footsteps.
So how does it work?
We use the Dual-shutter Camera (DSC) of Sheinin et al. to capture the tiny surface vibrations created by the impacting object at a sparse set of surface object points (marked by red circles below).
Source localization via backprojection.
(see paper for details)
As the elastic wave created by the impact reaches our measurement points, the DSC simultaneously measures the points' 2D surface tilts which relate to the instantaneous surface gradient directions. We show that during particular identifiable time intervals, called stable time intervals, these gradients point towards (or away) the impact source and can thus be used to recover its location on the surface. We developed a back-projection algorithm to recover the impact source locations.
What surfaces does our method support?
Our method assumes homogeneous surfaces. But these surfaces can be isotropic (e.g., plastic, fiberboard, or particleboard) or anisotropic, like wood. As shown in the animations above, an impact on isotropic materials creates circular waves, while in anisotropic materials, the wavefronts are approximately elliptical.
Our model can handle both cases (isotropic and anisotropic). For anisotropic materials, we can discover the anisotropic properties by knocking at several known positions.
What else can we learn from the measured vibrations?
We saw above that the wave's geometry lets us estimate the impact source. But the resulting elastic wave carries additional information about the disturbance. For instance, the preliminary experiment below demonstrates that the transient vibrations' magnitude (measured at a single point) has a square-root relation to the ball's dropping height. Since the maximal impact force has the same square root relation to the ball's height, our experiment suggests that the impact force, too, could be recovered from the transient vibrations.
Height effect on vibration magnitudes. Dropping a ping-pong ball from higher altitudes increases the vibration amplitudes via a square-root relation.
Similarly, the impacting object material properties also affect the spectral content of the resulting vibration. The experiment below shows that softer balls dropped from the same height created vibrations with a narrower spectral bandwidth than those generated by stiffer objects.
Object stiffness effect on vibration spectral composition.
Exciting future applications
Our method opens the door for various novel vision tasks like localizing sound sources in walls (e.g., pipe bursting), localizing bullet or bird impacts on airplanes mid-flight, or impacts on ship hulls from dockside, tugs, or other debris, localizing shellground impacts on battlefields, localizing people in building fires or hostage situations by observing external vibrations on ceilings or side walls, and more.


BibTex
@inproceedings{Zhang:2023,
title = {Analyzing Physical Impacts using Transient Surface Wave Imaging},
author={Zhang, Tianyuan and Sheinin, Mark and Chan, Dorian and Rau, Mark and O'Toole, Matthew
and Narasimhan, Srinivasa G.},
booktitle={Proc. IEEE CVPR},
year={2023},
}

